Sampling Importance Resampling(간단하게 Importance Resampling)은 임의의 분포로부터 샘플을 생성하는 알고리즘이다. 어떤 복잡한 분포든 evaluation만 가능하다면 그 분포에 근사하여 샘플을 생성할 수 있다.
정규화 되지 않은(unnormalized) 분포 $ \hat p $ 와 정규화된 분포(pdf) $p$를 생각해 보자.
\[\frac{\hat p}{C} = p\] \[C = \int_{\Omega} \hat p(x) dx\]앞으로 hat표시가 있는 $\hat p$ 는 정규화 되지 않은 분포, $p$는 정규화된 분포(pdf)로 구분해서 표기하겠다.
우리가 샘플링 하고싶은 target 분포는 정규화 되지 않은 $\hat p(x)$ 이다.
알고리즘
SIR 알고리즘으로 $p$를 근사하여 샘플을 생성하는 알고리즘은 다음과 같다.
- 샘플링 하기 쉬운 source pdf $q$로부터 $M \ge 1$ 개의 proposal 샘플을 생성한다.
- $\mathbf{x} = \{ x_1,…,x_M \}$
- 각 proposal 샘플마다 가충치 $w(x_i)$ 를 계산한다.
- $w(x) = \frac{\hat p(x)}{q(x)}$
- proposal 샘플의 가중치에 비례한 확률로 샘플 $x_z$을 다시 뽑는다. (Resampling)
- $ p(z \,|\, \mathbf{x}) = \frac{w(x_z)}{\sum_{i=1}^{M} w(x_i)},\, z \in \{1,…,M\} $
proposal 샘플의 가중치를 $w(x) = \frac{\hat p(x)}{q(x)}$ 로 설정한 부분이 핵심이다.
proposal 샘플은 $q$를 따르는 샘플이므로 $\mathbf{x}$에는 각 샘플이 $q(x_i)$에 비례한 만큼 존재한다. 여기서 가중치를 $q(x_i)$로 나눠줌으로써 이 시점에서 가중치($\frac{1}{q(x_i)}$)에 비례해 Resampling하면 모든 샘플을 동일한 확률로 뽑게 만든다. 여기에 다시 $\hat p(x)$ 을 곱하고 가중치 비례 Resampling을 하면 마침내 분포 $p$에 근사하여 샘플을 뽑을 수 있게 된다.
proposal 샘플의 수 $M$을 분포 보간 변수(distribution interpolation variable)로 볼 수 있다. $M \rightarrow \infty$ 갈수록 샘플의 분포는 $q$에서 $p$로 수렴한다.
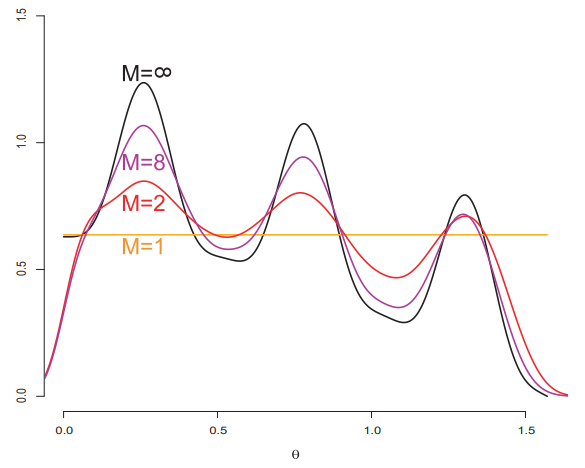1번 레퍼런스 Figure 2.1
RIS 논문에서 소개한 예시로 $q$는 uniform이고 $\hat p = cos(\theta) + sin^4(6\theta)$ 일 때 $M$이 점점 커짐에 따라 Resampling의 분포가 uniform($q$) 에서 $p$로 점점 다가간다.
SIR 알고리즘을 통해 생성된 샘플의 분포는 $q$와 $p$ 사이의 보간된, $p$에 근사하는 분포라는 부분을 잘 기억해야 한다. 정확히 $p$ 를 따르는 샘플이 아니다. 또한 SIR 알고리즘으로 생성된 샘플의 pdf는 알 수 없다. (논문에서 intractable 이라고 표현됨) 다시말해 resampling의 probability density는 unknown이다. ($M \rightarrow \infty$ 라면 $p(x_i)$ 다)
source pdf $q$ 가 $p$ 와 모양이 비슷할수록 수렴 속도가 더 빨라진다.
참조
[1] https://scholarsarchive.byu.edu/cgi/viewcontent.cgi?article=1662&context=etd
[2] https://blog.demofox.org/2022/03/02/sampling-importance-resampling/
[3] https://agraphicsguynotes.com/posts/understanding_the_math_behind_restir_di/#sample-importance-resampling-sir